Salinon

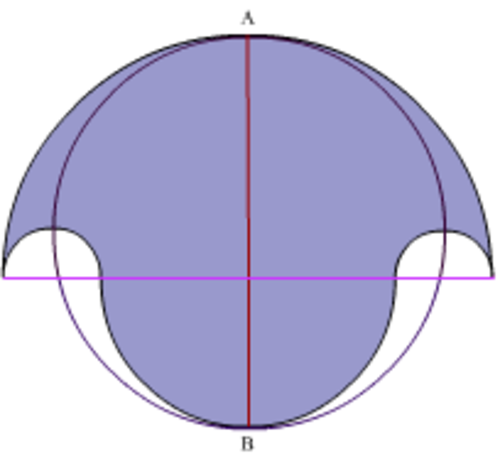
El salinon (que significa "salero" en griego) es una figura geométrica que consta de cuatro semicírculos. Se introdujo por primera vez en el Libro de los Lemas, un trabajo atribuido a Arquímedes.^[1]​

Construcción

Sea O el origen de un sistema de coordenadas cartesianas. Supóngase que A, D, E y B son cuatro puntos sobre la misma recta, en ese orden, sobre la línea de división O AB. Sea AD=EB. Los semicírculos se dibujan sobre la línea AB con diámetros AB, AD y EB, y se dibuja otro semicírculo por debajo con el diámetro DE. Un salinon es la figura delimitada por estos cuatro semicírculos.^[2]​

Propiedades

Área

Arquímedes introdujo el salinon en su "Libro de los Lemas" aplicando la Proposición 10 del Libro II de los Elementos de Euclides, señalando que "el área de la figura limitada por las circunferencias de todos los semicírculos [es] igual al área del círculo con diámetro CF".^[3]​

A saber, el área del salinon es:

${\displaystyle A={\frac {1}{4}}\pi \left(r_{1} r_{2}\right)^{2}.}$^[1]​

Demostración

Denótense los puntos medios de AD y EB como G y H, respectivamente. Por lo tanto, AG = GD = EH = HB = r₁. Debido a que DO, OF y OE son todos radios del mismo semicírculo, DO = OF = OE = r₂. Por adición de segmentos, AG   GD   DO = OE   EH   HB = 2r₁   r₂. Como AB es el diámetro del salinon, CF es un eje de simetría. Como todos son radios del mismo semicírculo, AO = BO = CO = 2r₁   r₂.

Sea P el centro del círculo grande. Dado que CO = 2r₁   r₂ y OF = r ₂, CF = 2r₁   2r₂, entonces el radio del círculo es r₁   r₂. El área del círculo = p (r₁   r₂)².

Sea x=r₁ e y=r₂. El área del semicírculo con diámetro AB, denotado por ${\displaystyle {\mathcal {A}}_{AB}}$, es:

${\displaystyle {\mathcal {A}}_{AB}={\frac {1}{2}}\pi \left(2x y\right)^{2}.}$

El área del semicírculo con diámetro DE es:

${\displaystyle {\mathcal {A}}_{DE}={\frac {1}{2}}\pi y^{2}.}$

El área de cada uno de los semicírculos con diámetros AD y EB es

${\displaystyle {\mathcal {A}}_{AD}={\mathcal {A}}_{EB}={\frac {1}{2}}\pi x^{2}.}$

Por lo tanto, el área del salinon es:

${\displaystyle {\frac {1}{2}}\pi \left(\left(2x y\right)^{2}-2x^{2} y^{2}\right)={\frac {1}{2}}\pi \left(2x^{2} 4xy 2y^{2}\right)=\pi \left(x^{2} 2xy y^{2}\right)=\pi \left(x y\right)^{2}=\pi \left(r_{1} r_{2}\right)^{2}}$

como queda demostrado.^[4]​

Arbelos

Si los puntos D y E convergen con O, formaría un arbelos, otra de las creaciones de Arquímedes, con simetría en respecto al eje vertical del sistema de coordenadas cartesianas.^[3]​

Véase también

• Cuadratura de la lúnula

Referencias

Enlaces externos

• L’arbelos. Parte II por Hamza Khelif en www.images.math.cnrs.fr de CNRS